4 steps of algorithm analysis and the time complexity of recursive algorithms

---

Algorithm Analysis

4 Steps

1、Problem statement 问题描述（要有明确的、量化的表述）

2、Algorithm design 算法设计（把主要的解决问题的思路(程序)等写出来、大家都知道的东西就可以不讲）

3、Algorithm analysis 算法分析 （给个指标(e.g. 时间复杂度$O(f(n))$)，衡量它有多快）

4、Discussion 讨论（改进or相关问题等）

Time Complexity: O(f(n))

Def

Let f be a function of n, we say X(n) is O(f(n)), if there is a constant c, such that X(n)<=cf(n) for all n>0.
//X(n)的阶不大于f(n)的阶Order

e.g.

Problem:

Given an array A[n], find the largest element in A[n].

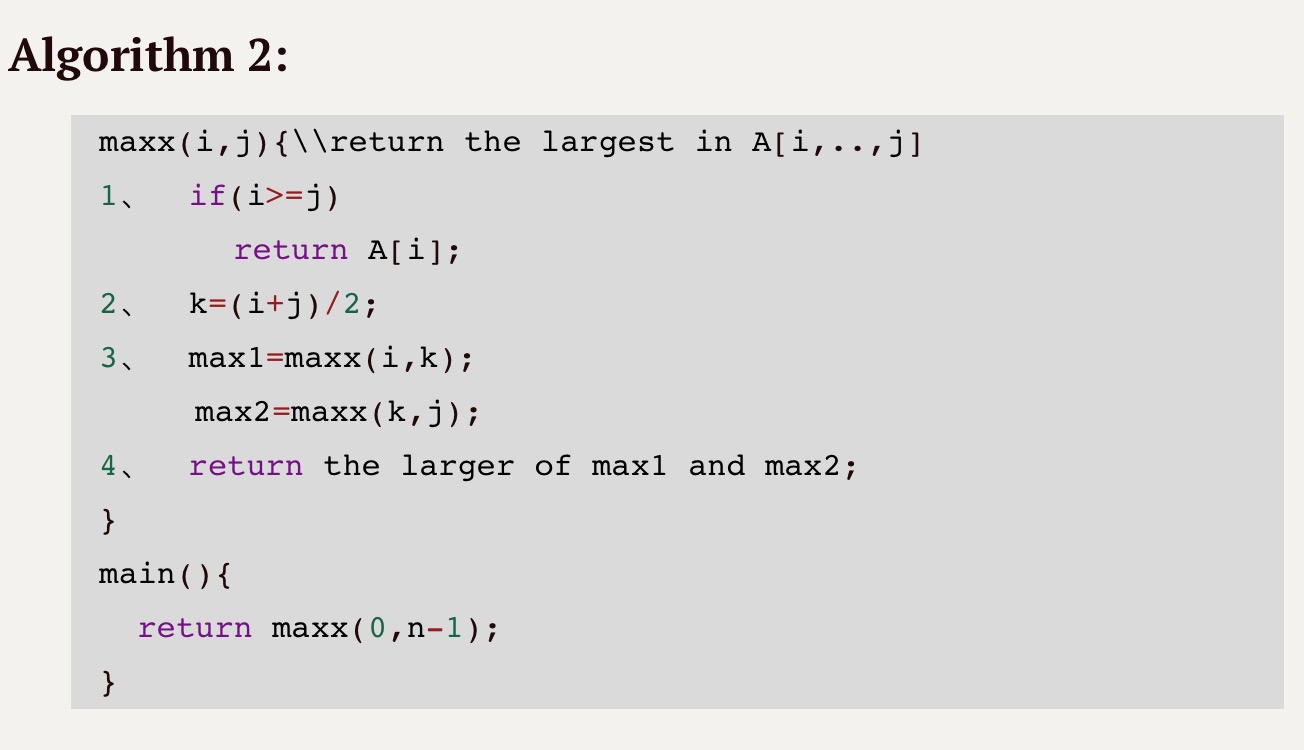
Analysis of recursive algorithms

1、assume the main algorithm runs in time T(n)

2、for each recursive call, replace its complexity by T(k), where k is the size of the input to the recursive call

3、write the recurrence relation: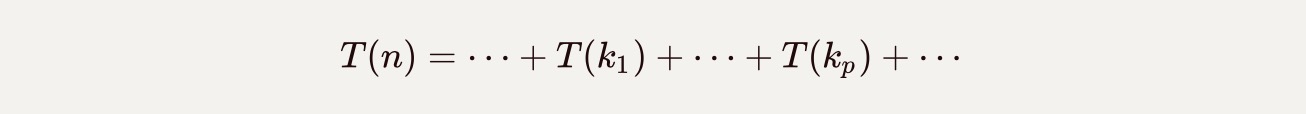

4、solve it

Analysis of Algorithm 2

Solve it

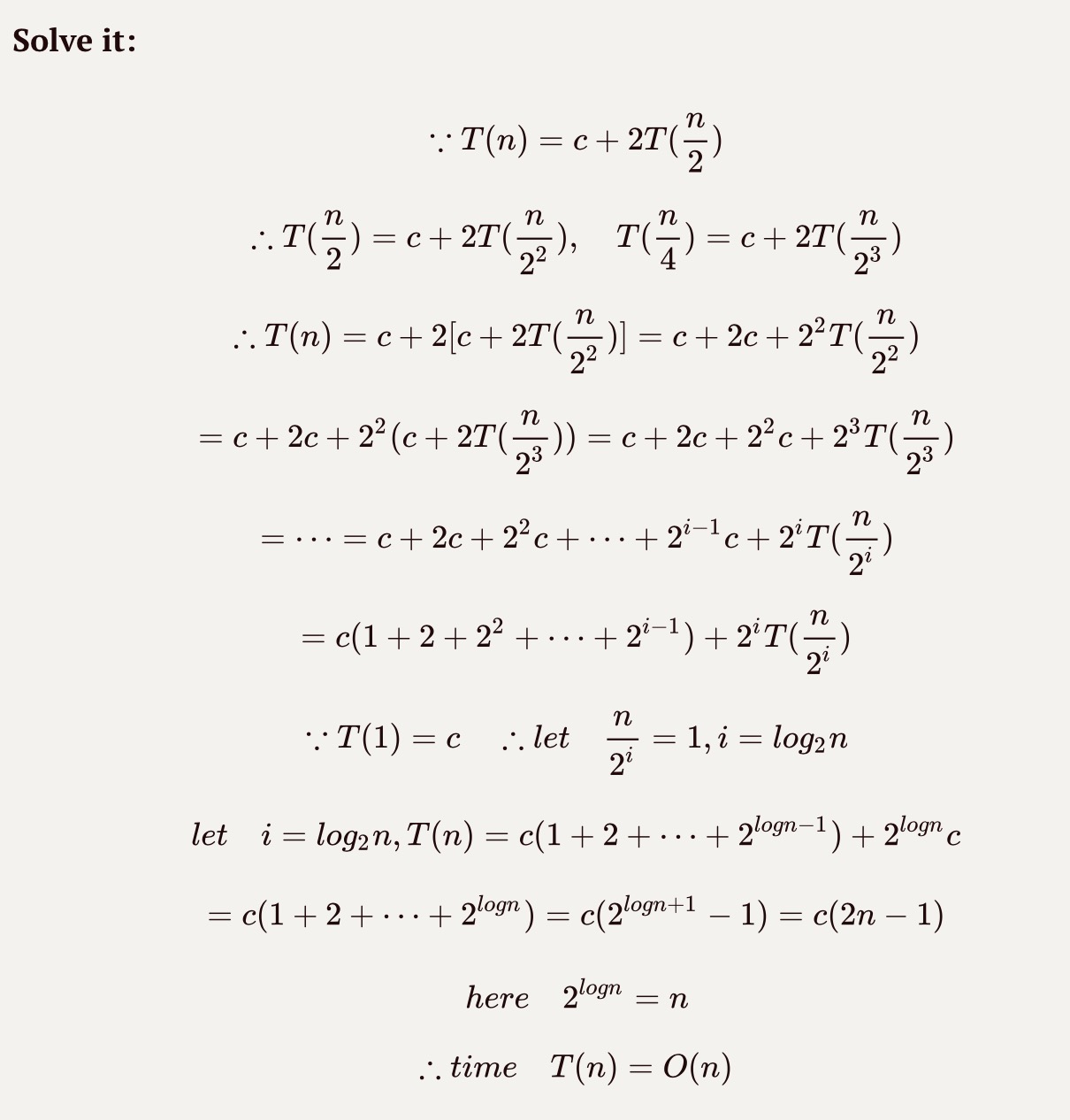
Discussion

Problem

1、n个乒乓球运动员，至少需要多少场比赛可以选出冠军？（n-1）

2、至少需要多少场比赛可以选出冠军和亚军？（n-1+log(n-1)）

Answers

1、从n个元素中选择最大的元素，用比较法，至少需要n-1次比较。所以，time=O(n)

2、从n个元素中选择前2个最大的元素：

(1) 用1、的方式：先选最大的元素，剔除它之后，再选第二大的元素，需要(n-1)+(n-1-1)=2n-3 次。所以，time=O(n)

(2) 先选最大的元素，再从所有和最大的元素比较过的元素中选择最大的元素(即为第二大的元素)，需要n-1+log(n-1)次。所以，time=O(n)

//先选冠军，再从所有被冠军打败的人中选择亚军
​