Dijkstra Algorithm

---

Graph Algorithms

G=(V,E)

V: set of vertices

E: set of edges

##图的表示法：

1、邻接矩阵 Adjacency Matrix: M[n] [n]

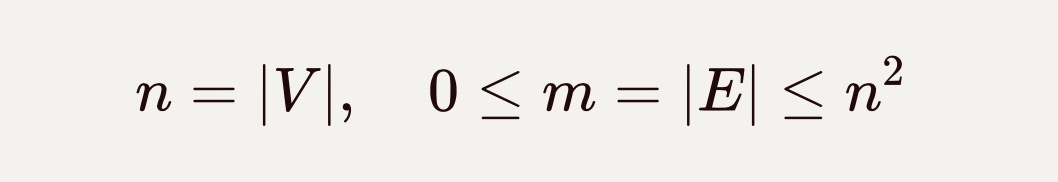
​ 无向图的邻接矩阵是对称的:

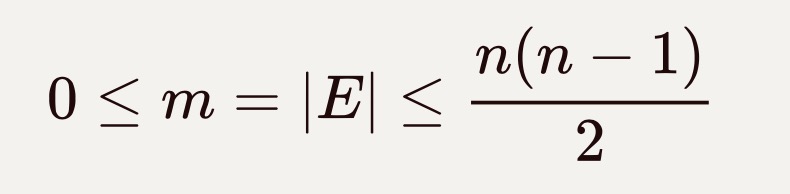
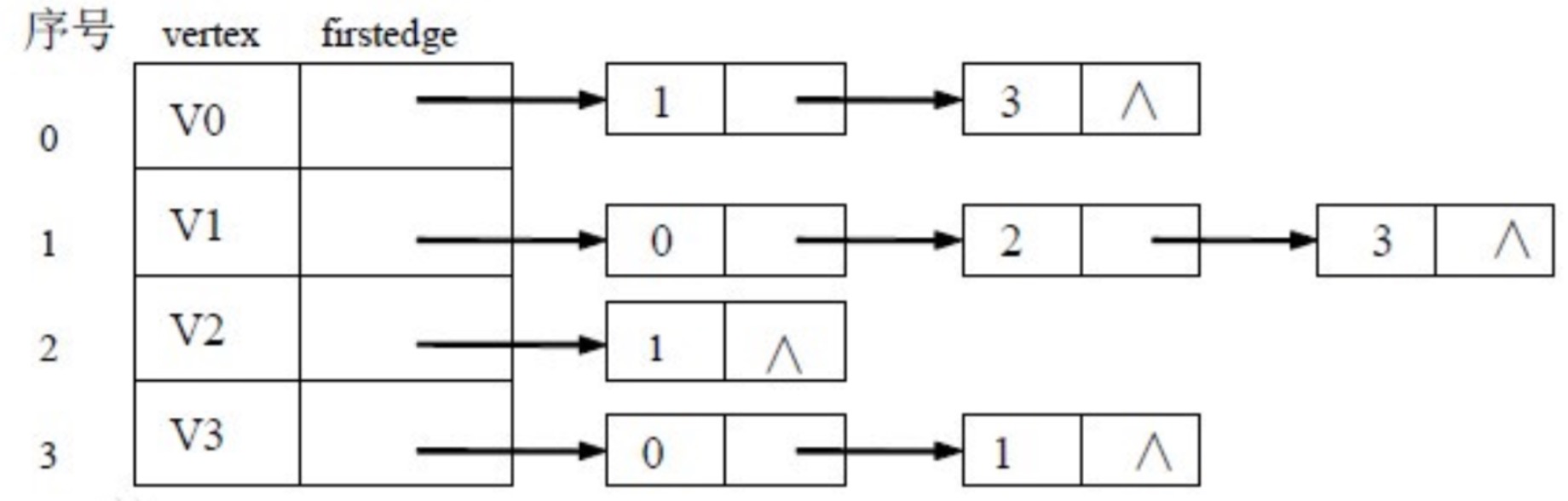
2、邻接链表 Adjacency List:

Problem: Shortest-Path

Given a graph (weighted graph) G and two vertices s and t, find a shortest path from s to t in G. Assume all edge weights are positive.

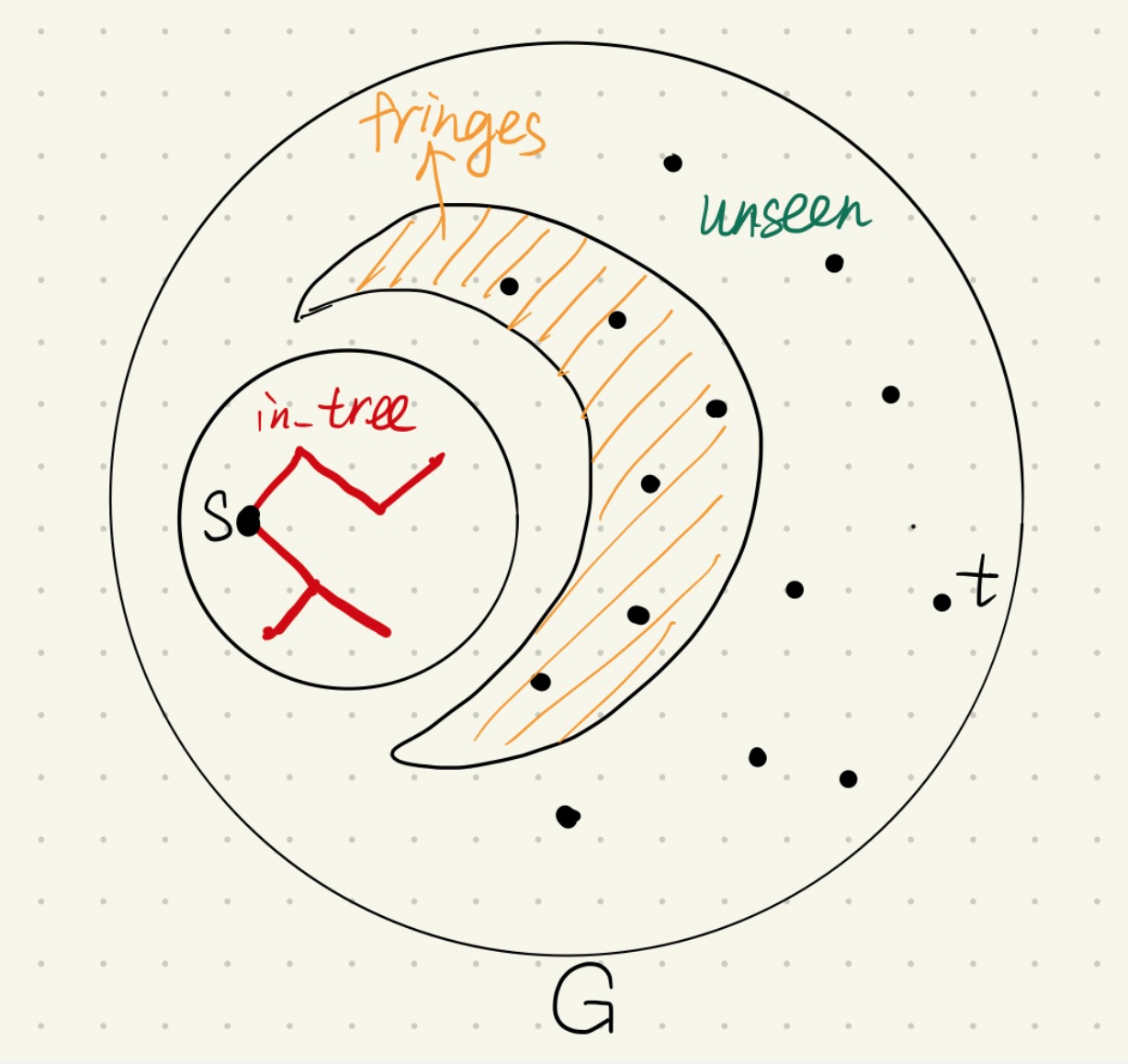
Dijkstra Algorithm

Single source shortest path

##Algorithm Analysis

1. O(n)
2. O(1)
3. O(n)
4. O(n^2)
5. O(1)

//花的时间最多的是4.，接下来详细分析一下4.

4. “while” run <= n times

   4.1 every “while” search for the smallest dist[·] needs O(n), so in 4. the whole time complexity for 4.1 is O(n^2);

   4.2 in 4. the whole time complexity for 4.2 is O(m), because 4.2 runs 2*m times in total.

So the time of Dijkstra is O(n^2).

Induction

​ To prove that a claim is true for all n>=1. //数学归纳法

3 steps：

​ Step 1: Verify the claim is true for n=1;

​ Step 2: Assume the claim is true for all k<n;

​ Step 1: Using the assume in step 2 to prove that the claim is true for n.

##Correctness(Proof)

Claim:

​ For each vertex v in in_tree, dist[v] is the distance of a shortest path from s to v, which can be computed using dad[·] (this is true when the number h of vertices in in_tree is any number).

Proof:

​ Step 1: h=1, s is in_tree, the claim holds true.

​ Step 2: Assume for k<h, the claim is true.

​ Step 3: Consider h. Let v be the h-th in_tree vertex, suppose v does not satisfy the claim.(反证法，假设从dad[·]算出来的不是最短的路径)

//todo

​ So, if all edge weights are positive, then Dijkstra Algorithm finds a shortest path from s to every vertex v with status[v]=in_tree.